Depois de um longo hiato devido à falta de tempo, o blog está de volta à ativa.
Um dos (muitos) motivos de minha ausência tem sido a elaboração do meu TCC, que é sobre previsão de demanda. Eu desenvolvi um sistema que seleciona automaticamente o melhor modelo de previsão dentre os disponíveis no pacote forecast para uma dada série temporal de acordo com a métrica de erro escolhida pelo usuário. O nome do pacote é mafs e já está disponível em meu Github para ser baixado e instalado gratuitamente. Notem, porém, que este é meu primeiro pacote R e eu provavelmente acabei cometendo muitos erros de principiante. Por isso, o pacote ainda é limitado e pode não funcionar em algumas situações que eu não vislumbrei. Uma possível limitação do pacote, por exemplo, é que ele só foi testado para séries mensais e não de outros períodos, como semanais, diárias ou trimestrais.
Demonstração do pacote
Apresentação e análise exploratória dos dados
Para demonstrar na prática como funciona o pacote, irei analisar neste post uma série temporal de periodicidade mensal referente ao volume de vendas do varejo, tema que tenho pesquisado recentemente e obtida no site do IBGE. O dataset será disponibilizado no repositório do blog.
# carregar bibliotecas importantes
library(mafs)
library(magrittr)
library(forecast)
library(ggplot2)
# importar dados
varejo <- read.csv2("/home/sillas/R/data/varejo.csv", stringsAsFactors = FALSE)
# exibir dados
head(varejo); tail(varejo)## Período Moveis.e.eletrodomesticos
## 1 jan/00 29.5
## 2 fev/00 28.4
## 3 mar/00 30.1
## 4 abr/00 28.8
## 5 mai/00 34.8
## 6 jun/00 30.5## Período Moveis.e.eletrodomesticos
## 185 mai/15 103.8
## 186 jun/15 91.6
## 187 jul/15 94.3
## 188 ago/15 91.1
## 189 set/15 90.2
## 190 NA# retirar última linha, que veio em branco
varejo <- varejo[1:(nrow(varejo)-1), ]Como pode-se ver, a série temporal vai desde Janeiro de 2000 a Setembro de 2015. Essa informação é importante para criar um objeto da class ts que será usado como input das funções do pacote mafs.
# transformar para série temporal
varejo <- ts(varejo[, 2], start = c(2000, 1), frequency = 12)
# Visualizar série
plot(varejo)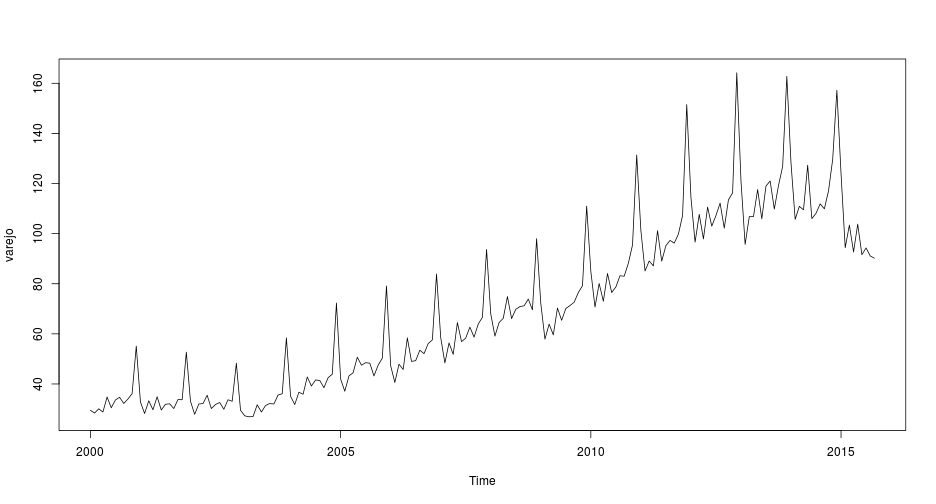
# Visualizar decomposição sazonal da série
varejo %>% decompose %>% plot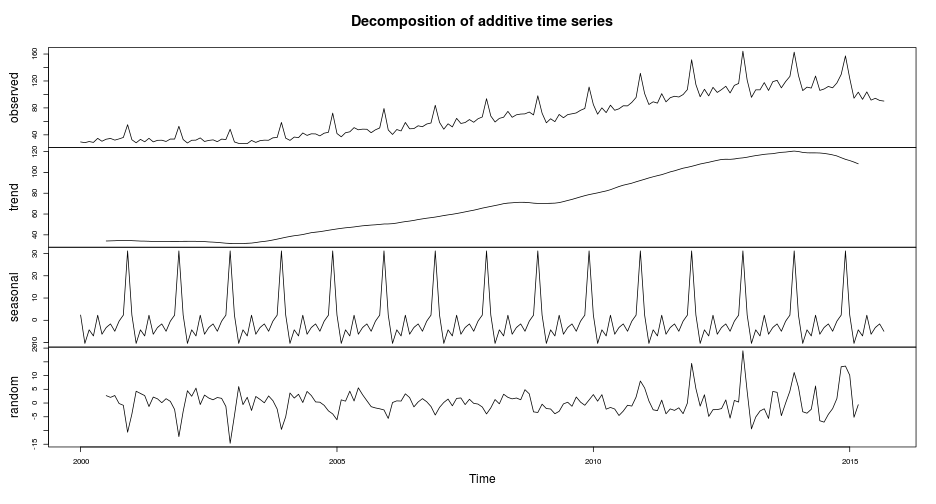
O gráfico da série decomposta mostra que há fortes componentes de tendência e sazonalidade na série. O componente aleatório possui média de 0,13, o que, por ser próxima a zero, nos leva a acreditar que a decomposição foi bem sucedida. O elemento sazonal da série também pode ser analisado nos gráficos a seguir.
# função ggmonthplot do pacote forecast
ggmonthplot(varejo)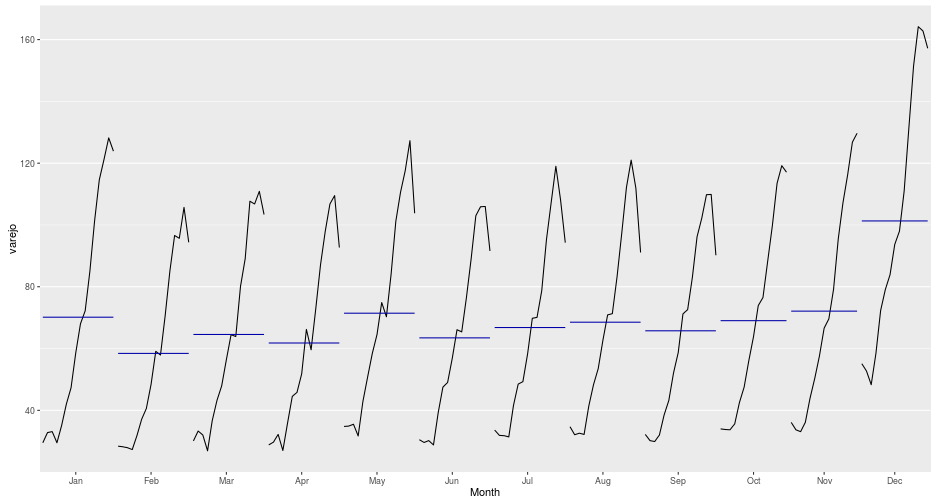
# estratificação por mês
ggseasonplot(varejo, year.labels = TRUE) + geom_point() + theme_bw()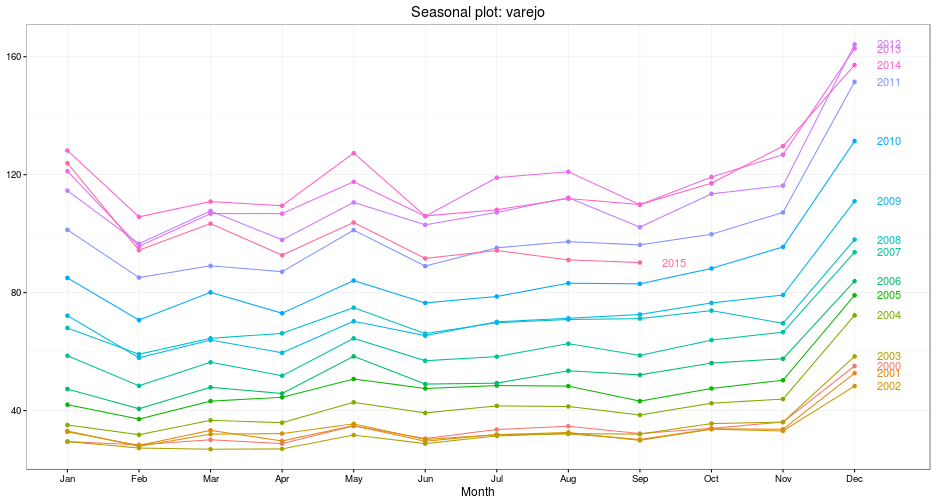
A partir dos dois gráficos é possível fazer uma observação interessante: A tendência é praticamente alternada. A série sempre cai de Janeiro a Fevereiro, sobe em Março, cai em Abril, sobe em Maio, cai em Junho, sobe ou se mantém estável em Julho, sobe em Agosto, cai ou se mantém estável em Setembro, e sobe de Outubro a Dezembro. A diferença mais evidente ocorrente entre os meses de Novembro e Dezembro.
Poderiam ser feitas mais algumas análises exploratórias, mas eu acabaria fugindo do escopo do post.
Aplicação do modelo.
O pacote mafs é um wrapper de diversos modelos presentes no pacote forecast, que são:
available_models()## [1] "auto.arima" "ets" "nnetar" "tbats" "bats"
## [6] "stlm_ets" "stlm_arima" "StructTS" "meanf" "naive"
## [11] "snaive" "rwf" "rwf_drift" "splinef" "thetaf"
## [16] "croston" "tslm" "hybrid"Cada um desses modelos pode ser aplicado à série temporal analisada por meio da função mafs::apply_selected_model(). Por exemplo, para o modelo de redes neurais, temos:
apply_selected_model(varejo, "nnetar", horizon = 6) %>% forecast(h = 6) %>% plot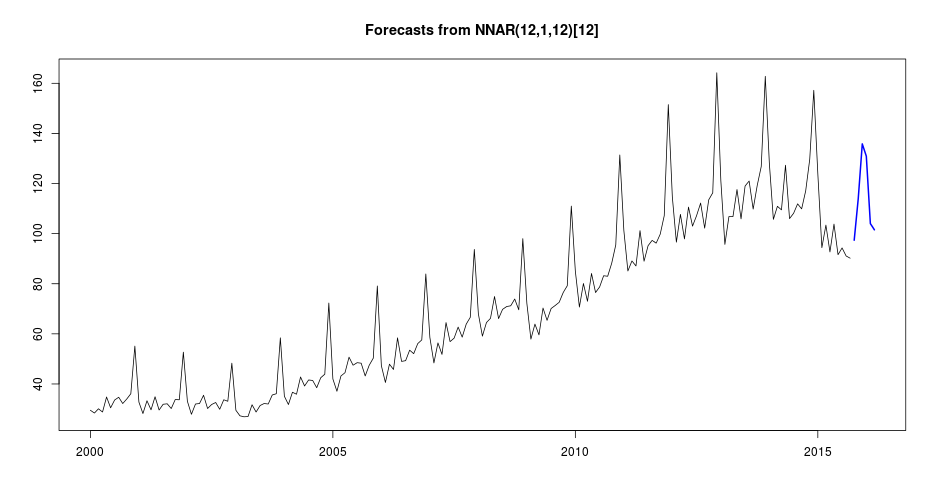
Imagine-se agora na situação onde vocë é um analista de previsão e precisa realizar, periodicamente, projeções de centenas ou milhares de séries temporais. Seria impraticável testar todos esses 18 modelos disponíveis, não seria? Pensando nisso, a principal função do mafs, chamada select_forecast() automatiza esse processo. Ela depende de quatro parâmetros:
x, que é a série temporal de input;test_size, que é o tamanho da série de teste a ser usado para mensurar a acurácia das previsões obtidas;horizon, o tamanho do horizonte de previsão;error, a métrica de erro para definir o melhor modelo.
O código da função pode ser conferido aqui. Resumidamente, ela separa a série de input em duas: a série de treino, usada para construir o ajuste dos modelos, e a série de teste, usada para mensurar a previsão obtida com os ajustes nas séries de treino em comparação com a série original. A partir das previsões obtidas, a de melhor acurácia (de acordo com a métrica escolhida pelo usuário) é selecionada para prever os valores futuros da série.
Após fazer tudo isso, a função retorna como output três objetos, como pode ser conferido em sua documentação (help("select_forecast")).
output <- select_forecast(varejo, test_size = 6, horizon = 6, error = "MAPE")## Fitting the auto.arima model
## Fitting the ets model
## Fitting the nnetar model
## Fitting the stlm model
## Fitting the tbats model# output com resultado de modelos
output$df_models## ME RMSE MAE MPE MAPE MASE ACF1
## 1 -11.876285 12.25375 11.876285 -12.63291 12.63291 1.683951 -0.24342789
## 2 -10.508709 11.15770 10.508709 -11.27795 11.27795 1.490041 0.40036466
## 3 -19.900878 22.41679 19.900878 -20.82833 20.82833 2.821766 -0.14176942
## 4 -12.403062 12.80147 12.403062 -13.24604 13.24604 1.758643 0.19773258
## 5 -13.824926 14.14055 13.824926 -14.80292 14.80292 1.960251 0.33411115
## 6 -17.702498 18.02916 17.702498 -18.98920 18.98920 2.510056 0.50385963
## 7 -21.315487 21.63862 21.315487 -22.84688 22.84688 3.022345 0.50840456
## 8 -14.823861 15.16935 14.823861 -15.77388 15.77388 2.101891 -0.26397115
## 9 25.496995 25.90687 25.496995 26.97627 26.97627 3.615245 -0.21035874
## 10 -9.450000 10.50579 9.583333 -10.30420 10.43265 1.358831 -0.21035874
## 11 -18.166667 18.49784 18.166667 -19.29829 19.29829 2.575871 -0.25244021
## 12 -9.450000 10.50579 9.583333 -10.30420 10.43265 1.358831 -0.21035874
## 13 -9.856044 10.87248 9.856044 -10.73736 10.73736 1.397499 -0.21035874
## 14 -26.141436 26.54988 26.141436 -28.11256 28.11256 3.706622 -0.18889000
## 15 -14.751994 15.18143 14.751994 -15.76853 15.76853 2.091701 0.19311316
## 16 -22.861101 23.31736 22.861101 -24.61078 24.61078 3.241499 -0.21035874
## 17 -25.849322 26.10141 25.849322 -27.70415 27.70415 3.665202 0.50145846
## 18 -13.782795 14.03367 13.782795 -14.71215 14.71215 1.954277 0.07285034
## model best_model
## 1 auto.arima naive
## 2 ets naive
## 3 nnetar naive
## 4 tbats naive
## 5 bats naive
## 6 stlm_ets naive
## 7 stlm_arima naive
## 8 StructTS naive
## 9 meanf naive
## 10 naive naive
## 11 snaive naive
## 12 rwf naive
## 13 rwf_drift naive
## 14 splinef naive
## 15 thetaf naive
## 16 croston naive
## 17 tslm naive
## 18 hybrid naive# output com valores previstos e reais
output$df_comparison## time forecasted observed
## 1 2015-04-03 103.4 92.7
## 2 2015-05-03 103.4 103.8
## 3 2015-06-02 103.4 91.6
## 4 2015-07-03 103.4 94.3
## 5 2015-08-02 103.4 91.1
## 6 2015-09-02 103.4 90.2# output com valores previstos, incluindo o intervalo de confiança de 80 e de 95%
output$best_forecast## Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
## Oct 2015 90.2 72.52035 107.8796 63.16131 117.2387
## Nov 2015 90.2 72.52035 107.8796 63.16131 117.2387
## Dec 2015 90.2 72.52035 107.8796 63.16131 117.2387
## Jan 2016 90.2 72.52035 107.8796 63.16131 117.2387
## Feb 2016 90.2 72.52035 107.8796 63.16131 117.2387
## Mar 2016 90.2 72.52035 107.8796 63.16131 117.2387O output de output$df_models mostra que o modelo de menor MAPE foi curiosamente o naive, que corresponde simplesmente a usar o último valor observado como previsão dos próximos valores. Tal previsão pode ser conferida visualmente com outra função do mafs, chamada gg_fit()
gg_fit(varejo, 6, "naive") + theme_bw() + theme(legend.position = "bottom")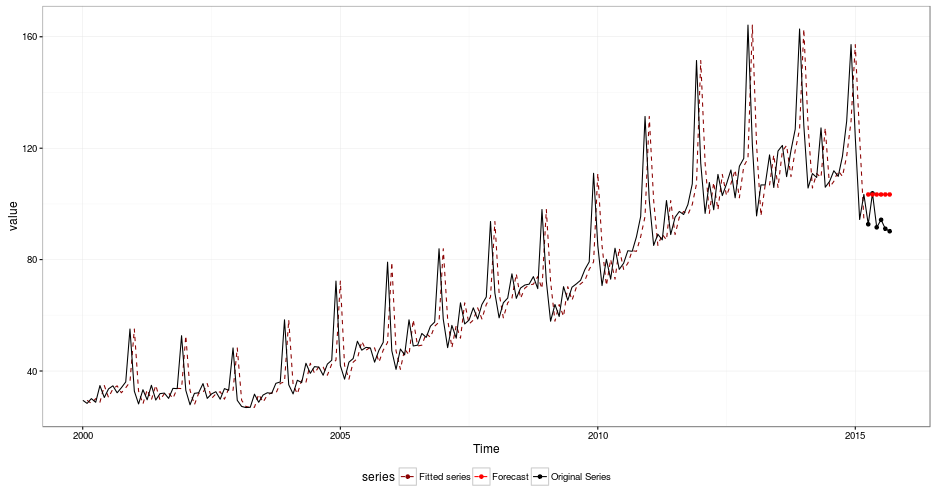
Para avaliar a eficiência do meu método, pode-se calcular o MAPE real, isto é, o erro relativo médio entre os valores previstos e os reais, presentes no objeto output$df_comparison
x <- output$df_comparison
# Calcular MAPE real
mape_real <- 100 * abs(x$forecasted - x$observed)/x$observed
# mostrar mape mês a mês
mape_real## [1] 11.5426106 0.3853565 12.8820961 9.6500530 13.5016465 14.6341463# mostrar mape médio
mean(mape_real)## [1] 10.43265Obtivemos um MAPE médio de 10,43%.
Ideias para o futuro
Devido à automatização possibilitada pelo pacote, é possível pensar em diversas outras análises e testes de hipóteses. Por exemplo: o tamanho da série influencia o desempenho do sistema? Isso poderia ser feito variando o argumento test_size, calculando o MAPE real para cada valor do argumento e depois comparando os resultados. Talvez isso tema de um futuro post.