Neste post, eu mostro como:
- Baixar dados de indicadores macroecômicos de todos os países usando a API do World Bank;
- Clusterizar países de acordo com esses indicadores usando o algoritmo k-means;
- O Brasil está mais próximo de Serra Leoa e Zimbábue que dos Estados Unidos e Noruega
library(WDI) # baixar os dados do World Bank
library(magrittr)
library(formattable)Importação dos dados
Felizmente, o processo de importação dos dados do World Bank é feito de maneira automatizada pelo pacote WDI usando a função WDI(). Como é necessário inserir o código do indicador, usei a função WDIsearch() para buscar o código do indicador relacionado a, por exemplo, inflação:
WDIsearch("Inflation")## indicator name
## [1,] "FP.CPI.TOTL.ZG" "Inflation, consumer prices (annual %)"
## [2,] "NY.GDP.DEFL.KD.ZG" "Inflation, GDP deflator (annual %)"Portanto, o código do indicador de inflação é “FP.CPI.TOTL.ZG”. Repeti o mesmo para outros indicadores que escolhi para esta análise:
# lista de indicadores para baixar:
lista_indicadores <- c("FP.CPI.TOTL.ZG", # inflação (%)
"NY.GDP.PCAP.CD", # Pib per capita (USD)
"NY.GDP.MKTP.KD.ZG", # crescimento do PIB anual (%),
"SL.UEM.TOTL.ZS" # Desemprego (%)
)
# Usei 2014 como ano de referência pois os resultados de alguns indicadores de 2015 ainda não foram disponibilizados
df <- WDI(indicator = lista_indicadores, country = "all", start = 2014, end = 2014, extra = TRUE)
str(df)## 'data.frame': 248 obs. of 14 variables:
## $ iso2c : chr "1A" "1W" "4E" "7E" ...
## $ country : chr "Arab World" "World" "East Asia & Pacific (developing only)" "Europe & Central Asia (developing only)" ...
## $ year : num 2014 2014 2014 2014 2014 ...
## $ FP.CPI.TOTL.ZG : num 2.78 2.6 3.86 2.53 6.67 ...
## $ NY.GDP.PCAP.CD : num 7447 10739 6240 6896 1504 ...
## $ NY.GDP.MKTP.KD.ZG: num 2.28 2.49 6.75 2.26 6.89 ...
## $ SL.UEM.TOTL.ZS : num 11.52 5.93 4.58 9.26 3.9 ...
## $ iso3c : Factor w/ 248 levels "ABW","AFG","AGO",..: 6 243 59 61 195 5 7 2 11 4 ...
## $ region : Factor w/ 8 levels "Aggregates","East Asia & Pacific (all income levels)",..: 1 1 1 1 1 3 5 7 4 3 ...
## $ capital : Factor w/ 211 levels "","Abu Dhabi",..: 1 1 1 1 1 10 2 80 167 191 ...
## $ longitude : Factor w/ 211 levels "","-0.126236",..: 1 1 1 1 1 45 141 169 158 72 ...
## $ latitude : Factor w/ 211 levels "","0.20618","-0.229498",..: 1 1 1 1 1 137 77 105 46 131 ...
## $ income : Factor w/ 7 levels "Aggregates","High income: nonOECD",..: 1 1 1 1 1 2 2 5 7 7 ...
## $ lending : Factor w/ 5 levels "Aggregates","Blend",..: 1 1 1 1 1 5 5 4 3 3 ...O output acima mostra que o data frame não contém dados apenas de países mas também de unidades agregadas, como o mundo, mundo árabe, América Latina, etc. Por isso, removi as unidades agregadas:
df$region %<>% as.character
# remover agregados
df <- subset(df, region != "Aggregates")Abaixo eu crio um novo dataframe apenas com as variáveis de interesse:
df2 <- df[, lista_indicadores]
row.names(df2) <- df$country
colnames(df2) <- c("inflacao", "pib_per_capita", "crescimento_pib", "desemprego")
summary(df2)## inflacao pib_per_capita crescimento_pib desemprego
## Min. :-1.5092 Min. : 255 Min. :-24.000 Min. : 0.300
## 1st Qu.: 0.5936 1st Qu.: 1802 1st Qu.: 1.588 1st Qu.: 4.300
## Median : 2.6705 Median : 5484 Median : 3.310 Median : 6.900
## Mean : 3.9496 Mean : 14625 Mean : 3.205 Mean : 8.606
## 3rd Qu.: 5.4123 3rd Qu.: 16091 3rd Qu.: 5.199 3rd Qu.:10.950
## Max. :62.1686 Max. :116613 Max. : 10.300 Max. :31.000
## NA's :39 NA's :27 NA's :29 NA's :38Duas observações importantes sobre o output acima:
- Para facilitar a interpretação dos resultados da análise, transformei a taxa de desemprego em taxa de emprego, pois assim temos três indicadores que. quanto maior seus valores, mais pujante é a Economia de seus países;
- Alguns países não contém dados para alguns dos indicadores. Não há informação, por exemplo, sobre desemprego em 38 países.
Para resolver o problema dos valores ausentes (os NA), poderia ser aplicada uma técnica robusta, mas como esta é uma análise simples ou optei por remover os países que tinham algum dado faltando.
df2 <- na.omit(df2)
df2$desemprego <- 100 - df2$desemprego
names(df2)[4] <- "emprego"Clusterização
Para usar o algoritmo k-means para clusterizar os países, é necessário:
- Calcular a distância (dissimilaridade) entre os países;
- Escolher o número de clusteres.
Para o cálculo da distância, temos um problema: as escalas das colunas são diferentes. Enquanto o PIB per capita é dado em dólares por pessoa e vão de 255 a 116,613, os outros são dados em porcentagem. Se não for feita nenhuma transformação dos dados, o PIB per capita terá um peso muito maior na clusterização dos dados que os outros indicadores.
Por isso, é necessário convertes todos os indicadores a uma escala única de média 0:
df2_escala <- scale(df2)
# Conferindo o output para o Brasil
df2_escala["Brazil", ]## inflacao pib_per_capita crescimento_pib emprego
## 0.5314139 -0.1864309 -1.2654843 0.2454973Na nova escala, temos que o Brasil apresenta inflação acima da média, PIB per capita abaixo da média, Crescimento do PIB abaixo da média (e olha que isso foi em 2014…) e taxa de emprego acima da média.
A determinação da quantidade de clusteres não segue uma regra pré-definida e deve ser pensada pelo responsável pela análise. Cada projeto de clusterização tem suas próprias particularidades. Contudo, alguns métodos analíticos podem ajudar nessa escolha, seja pela minização da soma dos quadrados dos clusteres ou pelo auxílio visual de um dendograma.
Para determinar o número de clusteres pelo primeiro método, observe o gráfico abaixo:
# referencia: http://www.statmethods.net/advstats/cluster.html
wss <- (nrow(df2_escala)-1)*sum(apply(df2_escala,2,var))
for (i in 2:15) wss[i] <- sum(kmeans(df2_escala,
centers=i)$withinss)
plot(1:15, wss, type="b", xlab="Número of Clusters",
ylab="Soma dos quadrados dentro dos clusteres") 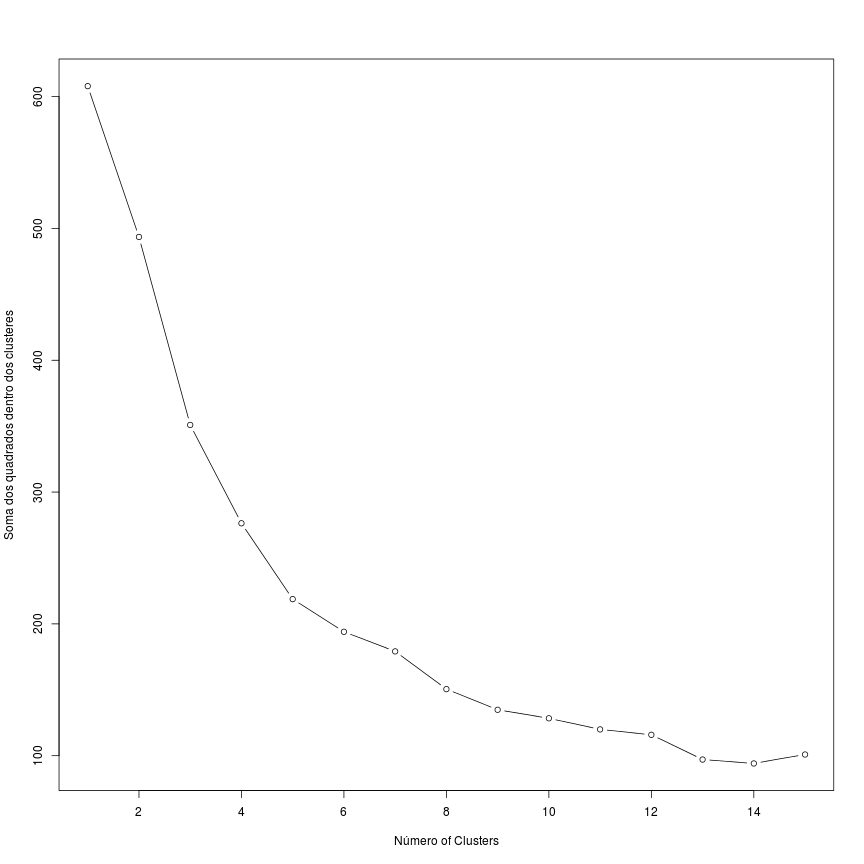
A soma dos quadrados dos clusteres se mantem estável a partir de 8 segmentos. Contudo, é preciso pensar qual a interpretação que teríamos disso. Quer dizer, posso dizer que dividi os dados em 8 clusteres, mas… e daí? O que seria aprendido por meio desses 8 clusteres?
Pelo segundo método, um dendograma é criado:
dendo <- df2_escala %>% dist %>% hclust
plot(dendo)
rect.hclust(dendo, k = 3, border = "blue")
rect.hclust(dendo, k = 4, border = "red")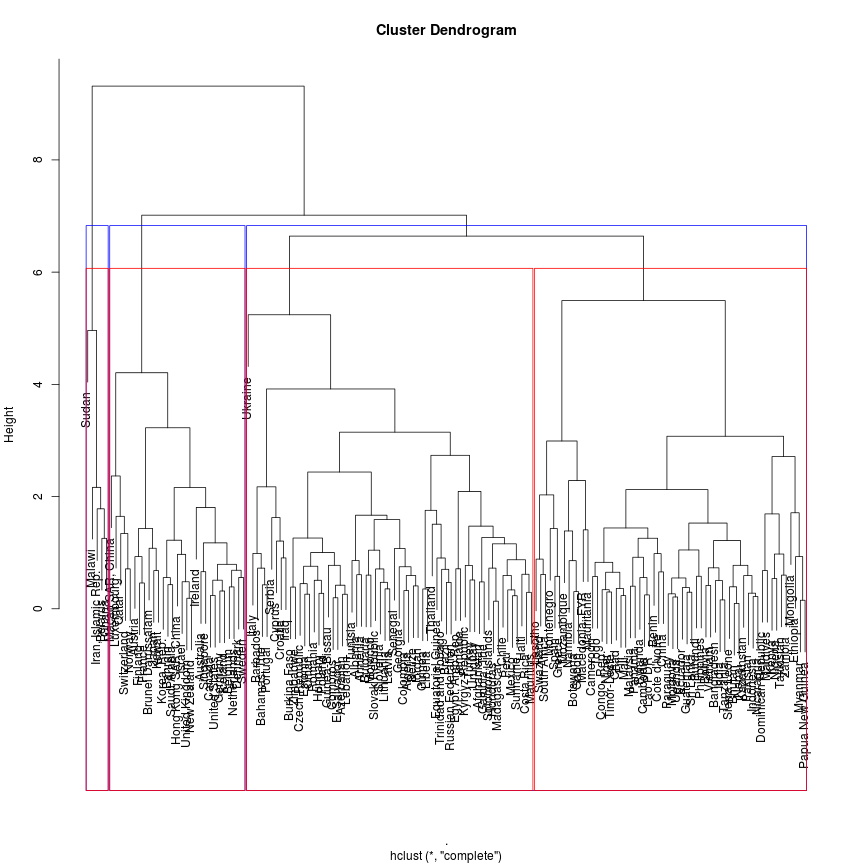
A posição de cada país no dendograma é determinada pela dissimilaridade entre cada um dos outros países. Veja que a opção de 4 segmentos divide um dos segmentos da opção de 3 ao meio. Portanto, 4 parece ser uma boa escolha para a quantidade de clusteres do modelo desta análise.
Por exemplo, esta é a distância entre o Brasil e alguns outros países:
df2_escala[c("Brazil", "Sierra Leone", "Zimbabwe", "Norway", "United States"),] %>% dist## Brazil Sierra Leone Zimbabwe Norway
## Sierra Leone 1.900431
## Zimbabwe 2.060580 1.650196
## Norway 4.060091 4.559608 4.400310
## United States 2.334771 2.866905 2.503331 1.970294Dá para ver que o Brasil tem uma distância euclidiana de 1,90 em relação a Serra Leoa, 2,06 ao Zimbábue, 2,33 aos Estados Unidos e 4,06 a Noruega. Ou seja, levando em conta os indicadores macroeconômicos considerados nesta análise, é possível dizer que o Brasil é mais similar com países miseráveis do que com países ricos (Veja como os EUA são menos distantes em relação a Noruega do que ao Zimbábue).
Podemos também ver qual a distribuição do grau de dissimularidade do Brasil com o resto do mundo:
mat_brasil <- df2_escala %>% dist(diag = TRUE, upper = TRUE) %>% as.matrix
# 5 países com menor dissimilaridade
mat_brasil[, "Brazil"] %>% sort() %>% head(6)## Brazil Russian Federation Equatorial Guinea
## 0.0000000 0.4703667 0.5118298
## Gambia, The Trinidad and Tobago Chile
## 0.5927519 0.7035814 0.8109536# 5 países com MAIOR dissimilaridade
mat_brasil[, "Brazil"] %>% sort() %>% tail(5)## Qatar Malawi Mauritania Luxembourg Sudan
## 4.282810 4.399952 4.756417 5.083102 6.676918O resultado dos 5 países mais distantes do Brasil é curioso: dentre eles, há 2 países ricos (Qatar e Luxemburgo) e três pobres (Malawi, Mauritânia e Sudão). Ou seja, não é necessariamente verdade que o Brasil é mais similar a países pobres da África que países ricos. Esse é o tipo de coisa que, se eu fosse um jornalista sensacionalista, omitiria.
Brincadeiras a parte, já podemos pular para a parte de criar os segmentos:
# fixar uma seed para garantir a reproducibilidade da análise:
set.seed(123)
# criar os clusteres
lista_clusteres <- kmeans(df2_escala, centers = 4)$cluster# função customizada para calcular a média dos indicadores para cada cluster
cluster.summary <- function(data, groups) {
x <- round(aggregate(data, list(groups), mean), 2)
x$qtd <- as.numeric(table(groups))
# colocar coluna de quantidade na segunda posição
x <- x[, c(1, 6, 2, 3, 4, 5)]
return(x)
}
(tabela <- cluster.summary(df2, lista_clusteres))## Group.1 qtd inflacao pib_per_capita crescimento_pib emprego
## 1 1 53 6.24 3131.17 5.89 94.47
## 2 2 27 1.47 57642.74 1.59 94.18
## 3 3 53 3.16 9476.58 2.28 92.44
## 4 4 20 2.20 10320.51 2.25 79.23Para melhorar a apresentação visual do output acima, usei o pacote formattable junto com uma função que criei para colorir de verde o valor caso seja superior ou igual à média do indicador e vermelho caso contrário.
colorir.valor <- function(x) ifelse(x >= mean(x), style(color = "green"), style(color = "red"))
nome_colunas <- c("Cluster", "Quantidade de países do cluster", "Taxa de Inflação (%)",
"PIB Per Capita (US$)","Crescimento anual do PIB (%)", "Taxa de Emprego (%)")
formattable(
tabela,
list(
pib_per_capita = formatter("span", style = x ~ colorir.valor(x)),
crescimento_pib = formatter("span", style = x ~ colorir.valor(x)),
emprego = formatter("span", style = x ~ colorir.valor(x))
), col.names = nome_colunas, format = "markdown", pad = 0
)| Cluster | Quantidade de países do cluster | Taxa de Inflação (%) | PIB Per Capita (US$) | Crescimento anual do PIB (%) | Taxa de Emprego (%) |
|---|---|---|---|---|---|
| 1 | 53 | 6.24 | 3131.17 | 5.89 | 94.47 |
| 2 | 27 | 1.47 | 57642.74 | 1.59 | 94.18 |
| 3 | 53 | 3.16 | 9476.58 | 2.28 | 92.44 |
| 4 | 20 | 2.20 | 10320.51 | 2.25 | 79.23 |
Temos, então, 4 grupos de países distintos:
- Cluster 1: Inflação acima da média, PIB per capita abaixo, crescimento acima, emprego acima: países em desenvolvimento;
- Cluster 2: Inflação abaixo da média, PIB per capita muito acima, crescimento abaixo, emprego acima: países ricos;
- Cluster 3: Inflação abaixo da média, PIB per capita abaixo, crescimento abaixo, semprego acima: países relativamente pobres, piores que os do Cluster 1;
- Cluster 4: Inflação abaixo da média, PIB per capita abaixo, crescimento abaixo, emprego muito abaixo: países pobres.
Para finalizar, qual é o cluster do Brasil e quais os outros países que estão no mesmo segmento?
df2$cluster <- lista_clusteres
df2["Brazil",]## inflacao pib_per_capita crescimento_pib emprego cluster
## Brazil 6.332092 11726.81 0.1033714 93.2 3cl_brasil <- df2["Brazil", ]$cluster
x <- df2[df2$cluster == cl_brasil, ]
x[order(-x$pib_per_capita),] %>% knitr::kable()| inflacao | pib_per_capita | crescimento_pib | emprego | cluster | |
|---|---|---|---|---|---|
| Korea, Rep. | 1.2724064 | 27970.4951 | 3.3101476 | 96.5 | 3 |
| Bahrain | 2.6511955 | 24855.2156 | 4.4809352 | 96.1 | 3 |
| Saudi Arabia | 2.6705256 | 24406.4765 | 3.6386990 | 94.4 | 3 |
| Slovenia | 0.2000749 | 24001.9014 | 3.0483310 | 90.5 | 3 |
| Trinidad and Tobago | 5.6844181 | 21323.7547 | 0.8171023 | 96.0 | 3 |
| Estonia | -0.1448155 | 20147.7782 | 2.9065372 | 92.3 | 3 |
| Czech Republic | 0.3371869 | 19502.4173 | 1.9781540 | 93.8 | 3 |
| Oman | 1.0140148 | 19309.6124 | 2.8942055 | 92.8 | 3 |
| Equatorial Guinea | 4.8250896 | 18918.2768 | -0.3040945 | 92.1 | 3 |
| Slovak Republic | -0.0761653 | 18500.6646 | 2.5219336 | 86.7 | 3 |
| Lithuania | 0.1064941 | 16489.7290 | 3.0324700 | 88.7 | 3 |
| Latvia | 0.6085193 | 15692.1916 | 2.3592052 | 90.0 | 3 |
| Barbados | 1.8871702 | 15366.2926 | 0.1803427 | 88.0 | 3 |
| Chile | 4.3950000 | 14528.3258 | 1.8940490 | 93.6 | 3 |
| Poland | 0.1069519 | 14336.7977 | 3.3340489 | 90.8 | 3 |
| Hungary | -0.2223151 | 14026.5744 | 3.6722200 | 92.2 | 3 |
| Russian Federation | 7.8128951 | 12735.9184 | 0.6404858 | 94.9 | 3 |
| Brazil | 6.3320923 | 11726.8059 | 0.1033714 | 93.2 | 3 |
| Turkey | 8.8545727 | 10515.0078 | 2.9141429 | 90.8 | 3 |
| Costa Rica | 4.5153127 | 10415.4444 | 3.5023522 | 91.7 | 3 |
| Mexico | 4.0186172 | 10325.6461 | 2.2307947 | 95.1 | 3 |
| Lebanon | 0.7497186 | 10057.8884 | 2.0000000 | 93.6 | 3 |
| Mauritius | 3.2176919 | 10016.6486 | 3.6000000 | 92.3 | 3 |
| Romania | 1.0689610 | 10000.0026 | 2.7773444 | 93.0 | 3 |
| Suriname | 3.3897457 | 9680.1159 | 1.8429092 | 94.4 | 3 |
| Colombia | 2.8778103 | 7903.9258 | 4.5525010 | 89.9 | 3 |
| Azerbaijan | 1.3850289 | 7886.4591 | 2.0000000 | 94.8 | 3 |
| Bulgaria | -1.4181227 | 7851.2654 | 1.5502287 | 88.4 | 3 |
| Peru | 3.2260468 | 6541.0306 | 2.3502537 | 95.8 | 3 |
| Ecuador | 3.5731279 | 6345.8407 | 3.6749821 | 95.4 | 3 |
| Thailand | 1.8903771 | 5977.3806 | 0.8656637 | 99.1 | 3 |
| Algeria | 2.9164064 | 5484.0668 | 3.8000000 | 90.5 | 3 |
| Jordan | 2.8915663 | 5422.5709 | 3.0963303 | 88.9 | 3 |
| Jamaica | 8.2900058 | 5106.0775 | 0.6877507 | 86.8 | 3 |
| Belize | 1.2013996 | 4831.1776 | 3.5833148 | 88.5 | 3 |
| Georgia | 3.0688121 | 4435.1927 | 4.7664424 | 86.6 | 3 |
| Tunisia | 4.9377353 | 4420.6984 | 2.6958334 | 86.7 | 3 |
| El Salvador | 1.1057751 | 4119.9920 | 1.9519442 | 93.8 | 3 |
| Egypt, Arab Rep. | 10.1458006 | 3365.7074 | 2.2287910 | 86.8 | 3 |
| Morocco | 0.4354565 | 3190.3104 | 2.4170812 | 89.8 | 3 |
| Ukraine | 12.1883657 | 3082.4614 | -6.8000082 | 92.3 | 3 |
| Honduras | 6.1292493 | 2434.8272 | 3.0852150 | 96.1 | 3 |
| Solomon Islands | 5.1659024 | 2024.1904 | 1.5074263 | 96.1 | 3 |
| Senegal | -1.0797448 | 1067.1318 | 4.7205396 | 90.0 | 3 |
| Zimbabwe | -0.2172862 | 931.1982 | 3.8482899 | 94.6 | 3 |
| Haiti | 4.5661735 | 824.1598 | 2.7498502 | 93.2 | 3 |
| Comoros | 0.5787475 | 810.0758 | 2.0616395 | 93.5 | 3 |
| Burkina Faso | -0.2580895 | 713.0639 | 3.9960447 | 96.9 | 3 |
| Afghanistan | 4.6043340 | 633.5692 | 1.3125309 | 90.9 | 3 |
| Guinea-Bissau | -1.5092446 | 567.8226 | 2.5402863 | 93.1 | 3 |
| Guinea | 9.7139773 | 539.6158 | 0.3999986 | 98.2 | 3 |
| Liberia | 9.8263580 | 457.8586 | 0.7011416 | 96.2 | 3 |
| Gambia, The | 5.9473749 | 441.2934 | 0.8774606 | 93.0 | 3 |
Dá para perceber que existe um problema com nosso resultado: No mesmo segmento, estão presentes a Coreia do Sul e países como Haiti e Zimbábue. Isso pode ser explicado por uma série de razões, como:
- O número e perfil dos indicadores macroeconômicos escolhidos não é bom o suficiente para determinar uma segmentação eficiente dos países;
- O número de clusteres deveria ser maior;
- Deveriam ser feitas apenas interações (escolhendo valores diferentes como argumento de
set.seed()) - O erro se deve a um erro aleatório, também chamado de ruído, do algoritmo k-means. Afinal de contas, como sabemos, nenhum modelo é perfeito.