Transparência (2): Qual o salário médio dos servidores federais?

Este é o segundo post da série de artigos sobre dados do Portal Transparência relativos a de servidores federais. Agora, o foco são os salários.
Outra pequena mudança é que, para os gráficos deste post, ao invés de usar o tema theme_economist(), usarei o theme_wsj(), também incluso no package ggthemes.

library(ggplot2)
library(stringr)
library(ggthemes)
library(dplyr)
library(ggrepel)

Por alguma razão além do meu entendimento, o Portal da Transparência arquiva os dados de salários em um arquivo separado do principal. Iremos agora importá-lo e juntá-lo com o data frame principal, criado no post anterior.

# Basicamente as únicas colunas que importam são a 3ª (ID do servidor) e a 6ª (remuneração bruta)
df <- read.csv2("/home/sillas/R/data/transparencia.csv", fileEncoding = "ISO-8859-15")

salarios <- read.csv2("/home/sillas/Downloads/20150831_Remuneracao.csv",
                      sep="\t", stringsAsFactors=FALSE) %>%  select(3, 6) 


names(salarios) <- c("ID_SERVIDOR_PORTAL", "SALARIO")

names(df) <- str_to_upper(names(df))
df <- merge(df, salarios, by="ID_SERVIDOR_PORTAL")
df$x <- 1


rm(salarios)

Primeiramente, vamos olhar como é a distribuição dos salários dos servidores federais.

ggplot(data=df, aes(x=SALARIO)) +
    geom_histogram(binwidth=1000) +
    scale_x_continuous(breaks=seq(0, 50000, by=5000)) +
    labs(title="Histograma dos salários\n dos servidores",
         x="Salário", y="Quantidade de servidores") +
  theme_wsj()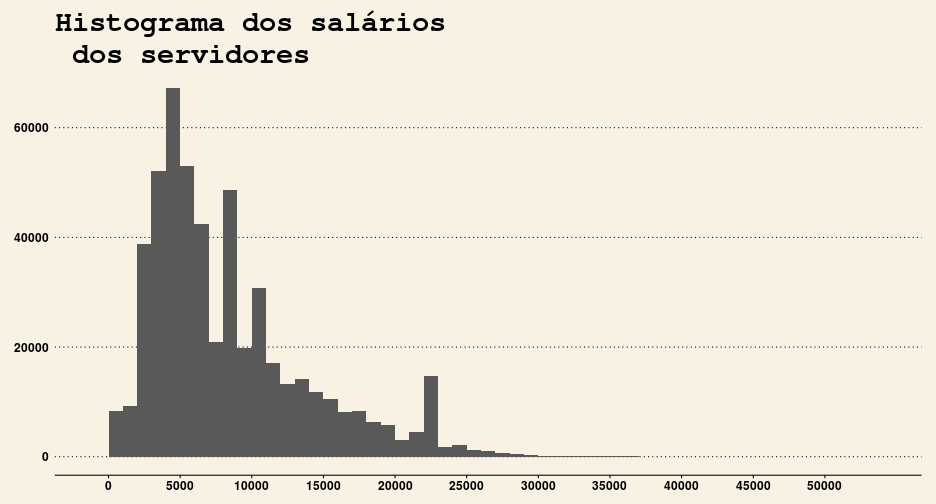

center

Com o gráfico acima, é possível aprender que:

Estranhamente, existe uma quantidade anormal (fora da curva) de servidores que ganham aproximadamente entre R$22.000 a RS$24.000,00.
Percebeu que existe um “breu” após a faixa dos 35000? É porque existem alguns poucos servidores que ganham acima disso, o que distorce o gráfico. Eles são nossos outliers.
Os salários dos servidores não seguem uma distribuição normal (ver comparação abaixo);

ggplot(data=df, aes(x=SALARIO)) +
    geom_histogram(binwidth=1000, aes(y=..density..)) +
    scale_x_continuous(breaks=seq(0, 50000, by=5000)) +
    labs(title="Distribuição dos salários\n dos servidores",
         x="Salário", y="Proporção") +
    stat_function(fun=dnorm, color="red", arg=list(mean=mean(df$SALARIO), sd=sd(df$SALARIO)))+
    theme_wsj()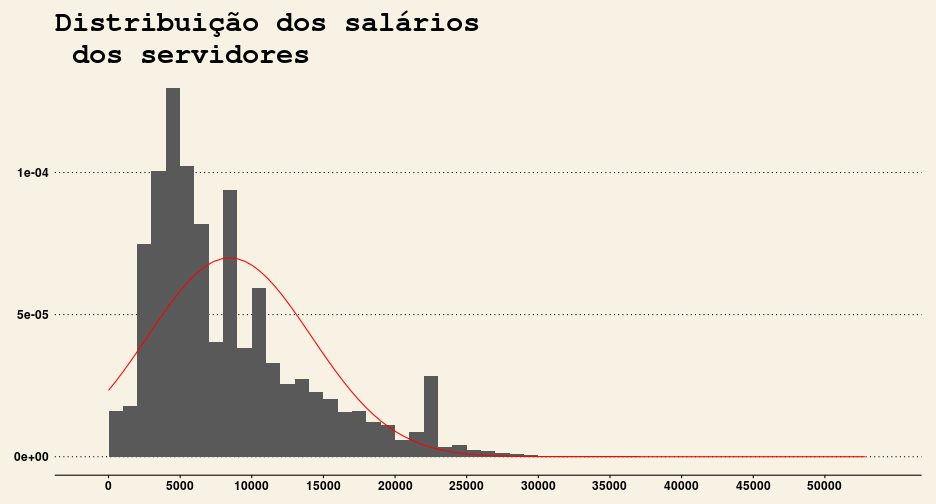

center

Será que os salários variam de acordo com a região? Existem diferentes visualizações que podem ser usadas para fazer essa comparação.

Histogramas

ggplot(data=df, aes(x=SALARIO)) +
  geom_histogram(binwidth=1000) +
  facet_grid(REGIAO~., scales = "free_y") +  #TESTE
  scale_x_continuous(breaks=seq(0, 50000, by=5000)) +
  theme_wsj() +
  labs(title = "Distribuição dos salários\n por região")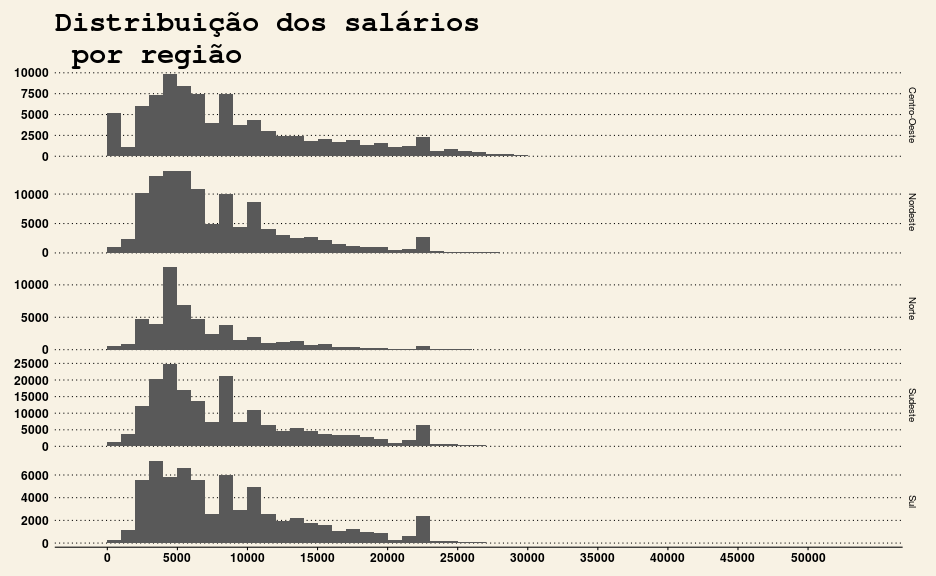

center

ggplot(data=df, aes(x=SALARIO)) +
    geom_histogram(binwidth=1000, aes(y=..density..)) +
    facet_grid(REGIAO~., scales = "free_y") + 
    scale_x_continuous(breaks=seq(0, 50000, by=5000)) +
    stat_function(fun=dnorm, color="red", arg=list(mean=mean(df$SALARIO), sd=sd(df$SALARIO)))+
    scale_y_continuous(breaks=NULL) +
    theme_wsj()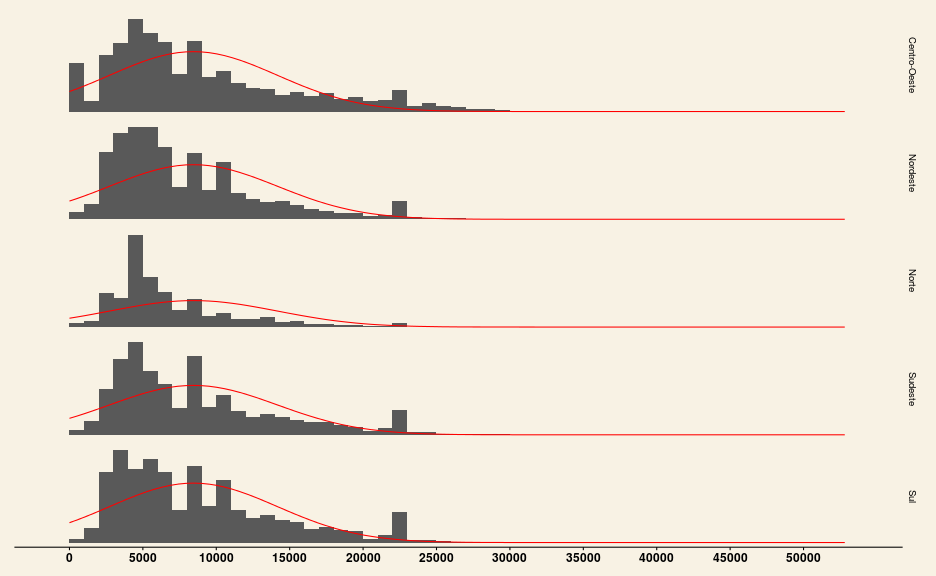

center

Com os gráficos acima, é possível inferir que:

A diferença entre as distribuições dos salários se mantém constante nas diferentes faixas salariais.
Na região Norte, existe uma quantidade anormalmente alta de pessoas que ganham por volta de 5000 reais.
No geral, os salários no Norte são bem baixos. A proporção de servidores que ganham acima de 10000 reais nessa região é muito menor que nas outras.

A distribuição dos salários da região Norte aparenta ser a que mais difere de uma distribuição normal. É possível quantificar essa diferença por meio de duas métricas:

Assimateria (skewness)

De acordo com Fonseca (2011) dá-se a nomenclatura de assimetria ao grau de afastamento de uma distribuição da unidade de assimetria. Uma Distribuição é Simétrica quando seus valores de Média, Mediana e Moda coincidem. A comparação entre o valor da Média e o valor da Moda, dá, portanto, uma indicação da inclinação da distribuição.

Curtose (kurtoses).

Dá-se o nome de curtose ao grau de achatamento da distribuição: (a) Quando a distribuição apresenta uma curva de frequência mais fechada (mais aguda em sua parte superior), ela é denominada Leptocúrtica (Lepto = Delgado, Alongado, Magro, etc.) (b) A distribuição de referência (Distribuição Normal) é denominada Mesocúrtica (Meso = Meio, Central, etc.). (c) Quando a distribuição apresenta uma curva de frequência mais aberta (mais achatada em sua parte superior), ela é denominada Platicúrtica (Plato = Chato, Plano, Largo, etc.).

Gráfico ou Diagrama de caixas (Boxplots)

Outra maneira de visualizar a variação da distribuição de uma variável contínua em diferentes categorias é por meio de gráficos de caixas.

O diagrama de caixa é uma ferramenta para localizar e analisar a variação de uma variável dentre diferentes grupos de dados. O diagrama de caixa procura obter as seguintes informações:

Calcular a mediana e os quartis ( o quartil inferior contém 25% ( 1/4) das menores medidas e o quartil superior contém 75 ( 3/4) de todas as medidas);

Plotar um símbolo onde se localiza a mediana e uma caixa, daí o nome de diagrama de caixas, onde a base representa o quartil inferior ( 25% ou 1/4) dos menores valores), e o topo da caixa o quartil superior (75% ou 3/4) dos valores observados. A caixa portanto representa 50% de todos os os valores observados ,concentrados na tendência central dos valores, eliminando os 25% menores valores e 25% maiores valores ( 75% - 25% = 50%);

Um segmento de reta vertical conecta o topo da caixa ao maior valor observado e outro segmento conecta a base da caixa ao menor valor observado, este segmento denomina-se Whisker, ou fio de bigode.

Fonte

Vamos analisar a distribuição de salários dos servidores de acordo com as regiões e os estados.

#1: Regiões
ggplot(data=df, aes(x=REGIAO, y=SALARIO, fill=REGIAO)) +
  geom_boxplot() +
  scale_fill_brewer(palette="Set1") +
  guides(fill=FALSE) +
  theme_wsj() +
  labs(title = "Distribuição dos salários por região")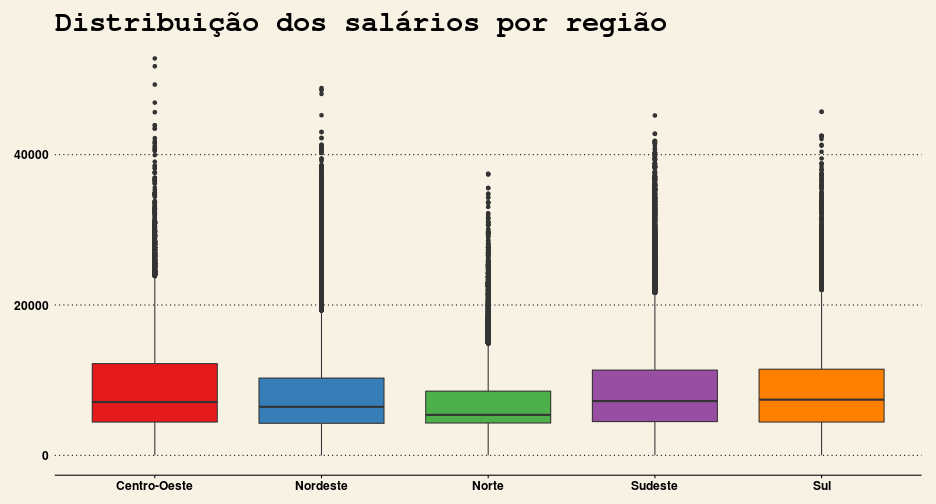

center

#2: Agrupar estados por região
# Defini um vetor de cores para cada estado para facilitar a visualização
coresEstados <- c(#Norte
                  "AM" = "#8dd3c7", "AP"="#ffffb3", "AC" = "#bebada",
                  "PA" = "#fb8072", "RO" = "#80b1d3", "RR" = "#fdb462",
                   #Nordeste
                  "AL" = "#8dd3c7", "BA" = "#ffffb3", "CE" = "#bebada",
                  "MA" = "#fb8072", "PB" = "#80b1d3", "PE" = "#fdb462",
                  "PI" = "#b3de69", "RN" = "#fccde5", "SE" = "#d9d9d9",
                  "TO" = "#bc80bd",
                  #CO
                  "DF" = "#8dd3c7", "GO" = "#ffffb3", "MS" = "#bebada", "MT" = "#fb8072",
                  #SUDESTE
                  "SP" = "#8dd3c7", "RJ" = "#ffffb3", "ES" = "#bebada", "MG" = "#fb8072",
                  #SUL
                  "PR" = "#b3de69", "SC" = "#fccde5", "RS" = "#d9d9d9"
                  )

ggplot(data=df, aes(x=UF_EXERCICIO, y=SALARIO, fill=UF_EXERCICIO)) + geom_boxplot() + facet_grid(. ~ REGIAO, scales="free_x") +
    scale_y_continuous(breaks=seq(0, 50000, by=5000)) + 
    scale_fill_manual(values= coresEstados) +
  theme_wsj() +
  labs(title = "Distribuição dos salários por estado") +
  guides(fill = FALSE)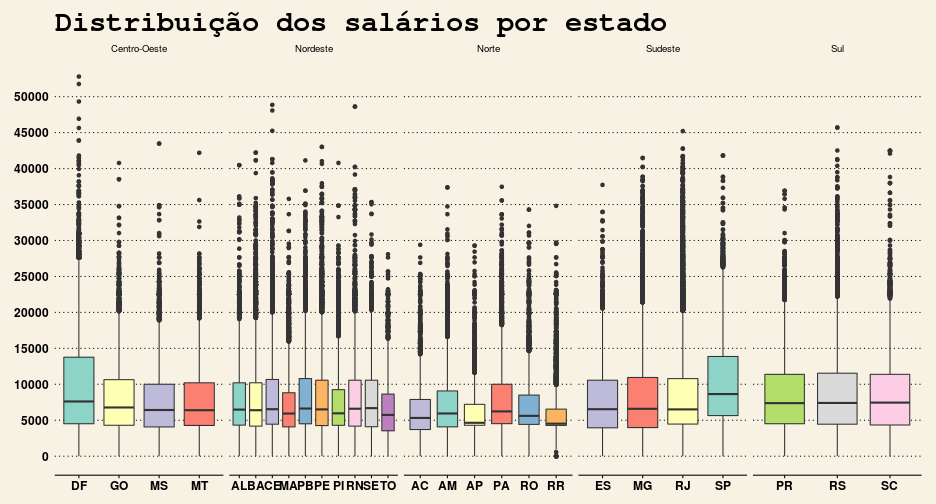

center

Por meio dos dois gráficos acima, aprendemos que:

A grande maioria dos outliers pertence ao Centro-Oeste, onde estão os três maiores salários de servidores do Brasil.
A “caixa” referente ao Norte é a mais achatada, o que mostra, mais uma vez, o quão anormalmente concentrada é a distribuição dos salários na região.
São Paulo aparenta ter o maior salário médio (calculado pela mediana), enquanto que Roraima e Amapá possuem os menores. Além disso, o salário médio paulista difere muito do observado em outros estados no Sudeste. De fato:

df %>%
  group_by(UF_EXERCICIO, REGIAO) %>%
  summarise(salarioMedio = round(median(SALARIO),0)) %>%
  ggplot(aes(x = salarioMedio, y = reorder(UF_EXERCICIO, salarioMedio))) +
  geom_point() +
  geom_segment(aes(yend = UF_EXERCICIO, xend = 0)) +
  facet_grid(REGIAO ~., drop = TRUE, scales = "free_y") +
  geom_text(aes(label = salarioMedio, hjust = -0.3)) +
  labs(title = "Salário médio por UF") +
  theme_wsj()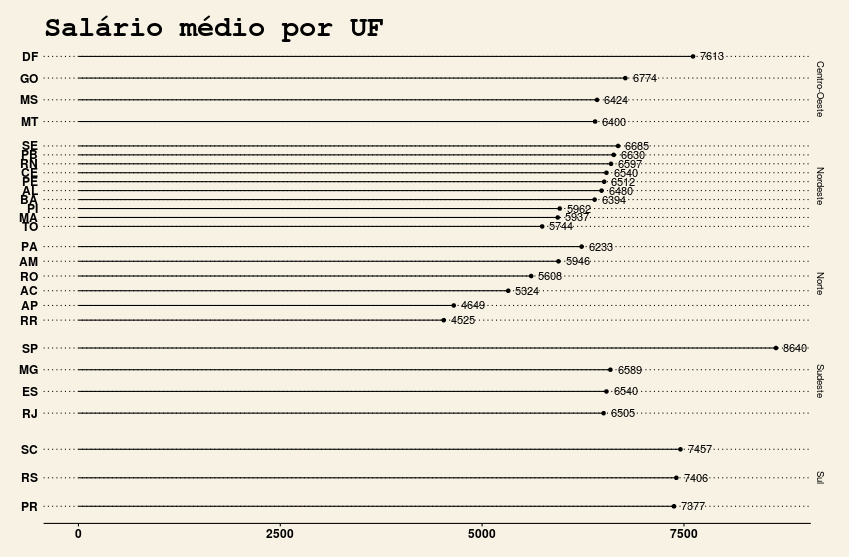

center

Será que existe alguma correlação entre o salário médio e o número de servidores do estado? Vamos tentar responder isso com um gráfico de dispersão comum, onde eu uso um recurso do package recém criado ggrepel:

temp <- df %>%
  group_by(UF_EXERCICIO) %>%
  summarise(salarioMedio = round(median(SALARIO),2),
            numeroDeServidores = n())

ggplot(temp, aes(numeroDeServidores, salarioMedio)) +
  geom_point() +
  geom_text_repel(aes(label = UF_EXERCICIO)) +
  geom_vline(xintercept = median(temp$numeroDeServidores)) +
  geom_hline(yintercept = median(df$SALARIO)) +
  labs(title = "Salário médio e número\n de servidores\n por estado", x = "Número de Servidores", y = "Salário Médio") +
  theme_wsj()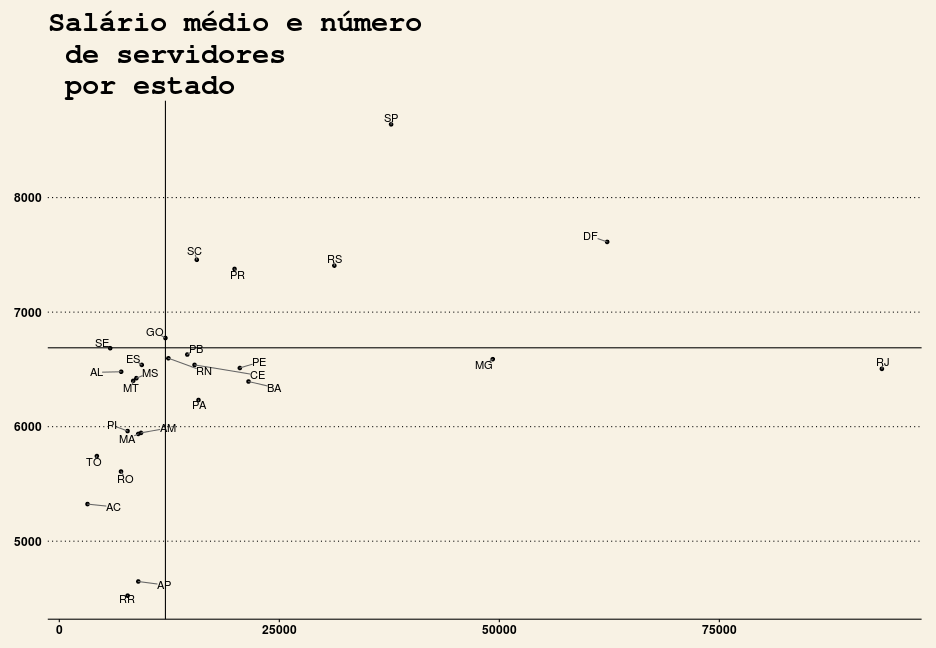

center

Não é possível detectar nenhum padrão muito significativo.

Nos vemos no próximo post!